Bella Subbotovskaya facts for kids
Quick facts for kids
Bella Abramovna Subbotovskaya
|
|
|---|---|
| Белла Абрамовна Субботовская | |

Subbotovskaya in 1961
|
|
| Born | December 17, 1937 |
| Died | November 23, 1982 (aged 44) |
| Cause of death | Car crash (suspected assassination) |
| Resting place | Vostryakovo Jewish Cemetery, Moscow |
| Nationality | Russian |
| Alma mater | Faculty of Mechanics and Mathematics, Moscow State University |
| Known for | Boolean formula complexity Jewish People's University |
| Spouse(s) |
Ilya Muchnik
(m. 1961–1971) |
| Scientific career | |
| Fields | Mathematical logic Mathematics education |
| Thesis | "A criterion for the comparability of bases for the realisation of Boolean functions by formulas" (1963) |
| Academic advisors | Oleg Lupanov |
Bella Abramovna Subbotovskaya (17 December 1937 – 23 September 1982) was a Soviet mathematician who founded the short-lived Jewish People's University (1978–1983) in Moscow. The school's purpose was to offer free education to those affected by structured anti-Semitism within the Soviet educational system. Its existence was outside Soviet authority and it was investigated by the KGB. Subbotovskaya herself was interrogated a number of times by the KGB and shortly thereafter was hit by a truck and died, in what has been speculated was an orchestrated accident.
Contents
Academic work
Prior to founding the Jewish People's University, Subbotovskaya published papers in mathematical logic. Her results on Boolean formulas written in terms of 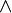 ,
, 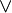 , and
, and  were influential in the then nascent field of computational complexity theory.
were influential in the then nascent field of computational complexity theory.
Random restrictions
Subbotovskaya invented the method of random restrictions to Boolean functions. Starting with a function 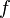 , a restriction
, a restriction 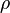 of
of 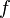 is a partial assignment to
is a partial assignment to  of the
of the 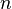 variables, giving a function
variables, giving a function 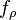 of fewer variables. Take the following function:
of fewer variables. Take the following function:
 .
.
The following is a restriction of one variable
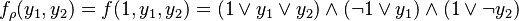 .
.
Under the usual identities of Boolean algebra this simplifies to  .
.
To sample a random restriction, retain 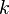 variables uniformly at random. For each remaining variable, assign it 0 or 1 with equal probability.
variables uniformly at random. For each remaining variable, assign it 0 or 1 with equal probability.
Formula Size and Restrictions
As demonstrated in the above example, applying a restriction to a function can massively reduce the size of its formula. Though 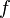 is written with 7 variables, by only restricting one variable, we found that
is written with 7 variables, by only restricting one variable, we found that 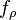 uses only 1.
uses only 1.
Subbotovskaya proved something much stronger: if 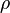 is a random restriction of
is a random restriction of  variables, then the expected shrinkage between
variables, then the expected shrinkage between 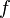 and
and 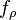 is large, specifically
is large, specifically
![\mathbb{E} \left [ L(f_\rho) \right ] \le \left ( \frac k n \right )^{3/2} L(f)](/images/math/d/e/4/de4f6436db1ca46c67fde201cef3c3f0.png) ,
,
where 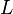 is the minimum number of variables in the formula. Applying Markov's inequality we see
is the minimum number of variables in the formula. Applying Markov's inequality we see
![\Pr \left [ L(f_\rho) \le 4 \left ( \frac k n \right )^{3/2} L(f) \right ] \ge \frac 3 4](/images/math/2/8/0/280f4e2a55f96e82bc8110e50b74408f.png) .
.
Example application
Take 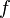 to be the parity function over
to be the parity function over 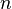 variables. After applying a random restriction of
variables. After applying a random restriction of  variables, we know that
variables, we know that 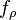 is either
is either 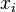 or
or 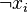 depending the parity of the assignments to the remaining variables. Thus clearly the size of the circuit that computes
depending the parity of the assignments to the remaining variables. Thus clearly the size of the circuit that computes 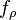 is exactly 1. Then applying the probabilistic method, for sufficiently large
is exactly 1. Then applying the probabilistic method, for sufficiently large 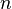 , we know there is some
, we know there is some 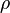 for which
for which
 .
.
Plugging in 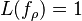 , we see that
, we see that 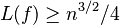 . Thus we have proven that the smallest circuit to compute the parity of
. Thus we have proven that the smallest circuit to compute the parity of 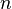 variables using only
variables using only  must use at least this many variables.
must use at least this many variables.
Influence
Although this is not an exceptionally strong lower bound, random restrictions have become an essential tool in complexity. In a similar vein to this proof, the exponent 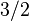 in the main lemma has been increased through careful analysis to
in the main lemma has been increased through careful analysis to 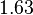 by Paterson and Zwick (1993) and then to
by Paterson and Zwick (1993) and then to 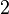 by Håstad (1998). Additionally, Håstad's Switching lemma (1987) applied the same technique to the much richer model of constant depth Boolean circuits.
by Håstad (1998). Additionally, Håstad's Switching lemma (1987) applied the same technique to the much richer model of constant depth Boolean circuits.
See also
 In Spanish: Bela Subbotovskaya para niños
In Spanish: Bela Subbotovskaya para niños

