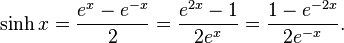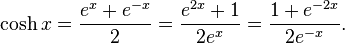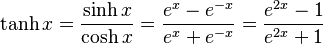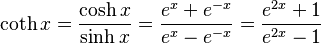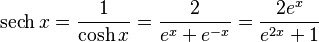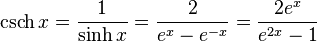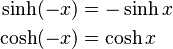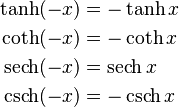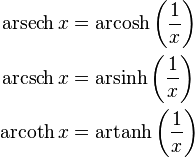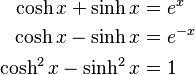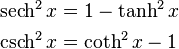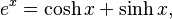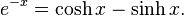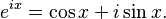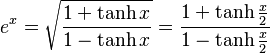Hyperbolic functions facts for kids
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined for the unit hyperbola rather than on the unit circle: just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the hyperbola.
Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. They also occur in the solutions of many linear differential equations, cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics.
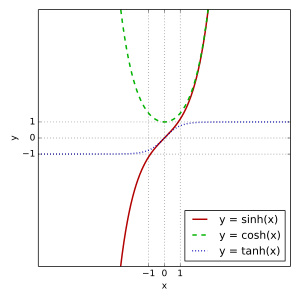
The basic hyperbolic functions are:
- hyperbolic sine "sinh",
- hyperbolic cosine "cosh",
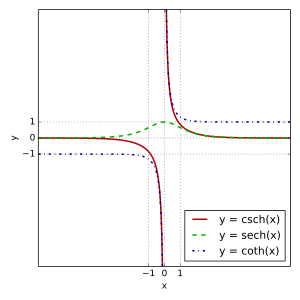
from which are derived:
- hyperbolic tangent "tanh",
- hyperbolic cosecant "csch" or "cosech"
- hyperbolic secant "sech",
- hyperbolic cotangent "coth",
corresponding to the derived trigonometric functions.
The inverse hyperbolic functions are:
- area hyperbolic sine "arsinh" (also denoted "sinh−1", "asinh" or sometimes "arcsinh")
- area hyperbolic cosine "arcosh" (also denoted "cosh−1", "acosh" or sometimes "arccosh"
- and so on.
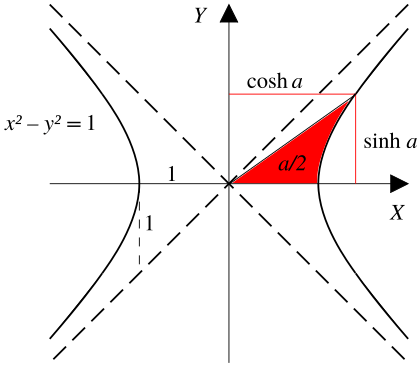
The hyperbolic functions take a real argument called a hyperbolic angle. The size of a hyperbolic angle is twice the area of its hyperbolic sector. The hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector.
Hyperbolic functions were introduced in the 1760s independently by Vincenzo Riccati and Johann Heinrich Lambert.
Contents
Definitions
There are various equivalent ways to define the hyperbolic functions.
Exponential definitions
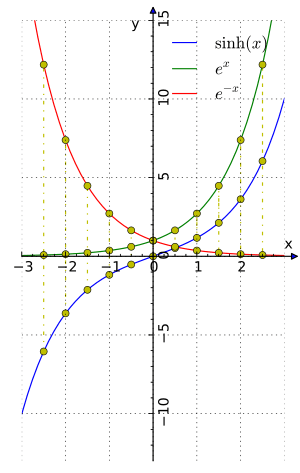
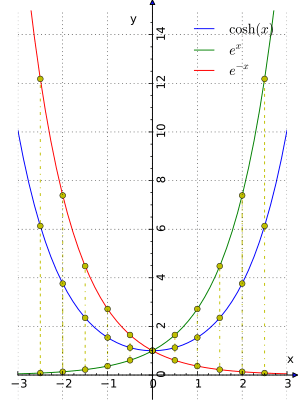
In terms of the exponential function:
- Hyperbolic sine: the odd part of the exponential function, that is
- Hyperbolic cosine: the even part of the exponential function, that is
- Hyperbolic tangent:
- Hyperbolic cotangent: for x ≠ 0,
- Hyperbolic secant:
- Hyperbolic cosecant: for x ≠ 0,
Useful relations
The hyperbolic functions satisfy many identities, all of them similar in form to the trigonometric identities.
Odd and even functions:
Hence:
Thus, cosh x and sech x are even functions; the others are odd functions.
Hyperbolic sine and cosine satisfy:
the last of which is similar to the Pythagorean trigonometric identity.
One also has
for the other functions.
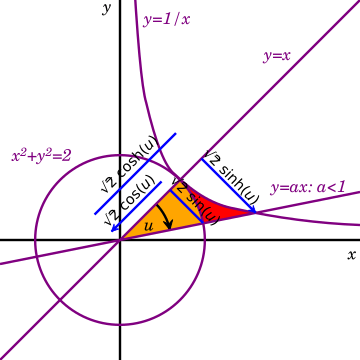
Comparison with circular functions
The hyperbolic functions represent an expansion of trigonometry beyond the functions defined on unit circle. Both types depend on one argument, either circular angle or hyperbolic angle.
Since the area of a circular sector with radius r and angle u (in radians) is r2u/2, it will be equal to u when r = √2. In the diagram, such a circle is tangent to the hyperbola xy = 1 at (1,1). The yellow sector depicts an area and angle magnitude. Similarly, the yellow and red sectors together depict an area and hyperbolic angle magnitude.
The legs of the two right triangles with hypotenuse on the ray defining the angles are of length √2 times the circular and hyperbolic functions.
Relationship to the exponential function
The decomposition of the exponential function in its even and odd parts gives the identities
and
The first one is analogous to Euler's formula
Additionally,
See also
 In Spanish: Función hiperbólica para niños
In Spanish: Función hiperbólica para niños