Image: SIR model anim

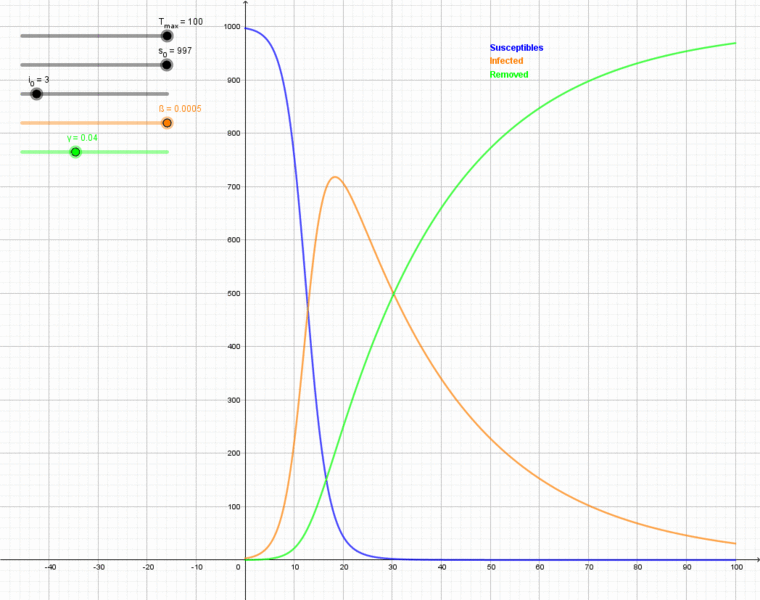
Description: Animation of the SIR model with initial values S(0)=997{\displaystyle S(0)=997}, I(0)=3{\displaystyle I(0)=3}, R(0)=0{\displaystyle R(0)=0}, and rate of recovery γ=0.04{\displaystyle \gamma =0.04}. The animation shows the effect of reducing the rate of infection from β=0.5{\displaystyle \beta =0.5} to β=0.12{\displaystyle \beta =0.12}. If there is no medicine or vaccination available, it is only possible to reduce the infection rate (often referred to as "flattening the curve") by appropriate measures such as social distancing. System of differential equations used for this model: dSdt=−β⋅S(t)⋅I(t){\displaystyle {\frac {dS}{dt}}=-\beta \cdot S(t)\cdot I(t)} dIdt=β⋅S(t)⋅I(t)−γ⋅I(t){\displaystyle {\frac {dI}{dt}}=\beta \cdot S(t)\cdot I(t)-\gamma \cdot I(t)} dRdt=γ⋅I(t){\displaystyle {\frac {dR}{dt}}=\gamma \cdot I(t)} This animation was created with GeoGebra by computing the numerical solutions of the system of differential equations. The core part of the construction is as follows: #################################### # system of differential equations # #################################### S'(t, S, I, R) = -ß I S I'(t, S, I, R) = ß S I - γ I R'(t, S, I, R) = γ I ############################################################### # numerical solutions of the system of differential equations # ############################################################### NSolveODE[{S', I', R'}, 0, {s_0, i_0, r_0}, T_{max}] # Result: # numericalIntegral1 -> S # numericalIntegral2 -> I # numericalIntegral3 -> R Note: Some authors use modified, but equivalent forms of the ODEs. Unfortunately, the same parameters are sometimes used. Example for the first ODE, where the infection rate is named β~{\displaystyle {\tilde {\beta }}} for the sake of clarity: dSdt=−β~N⋅S(t)⋅I(t){\displaystyle {\frac {dS}{dt}}=-{\frac {\tilde {\beta }}{N}}\cdot S(t)\cdot I(t)} By substituting β=β~N{\displaystyle \beta ={\tfrac {\tilde {\beta }}{N}}}, you get the same ODE as above. N{\displaystyle N} is a constant value (invariant of the model) and not needed for the ODE; in fact, the implementation didn't even use a variable for N{\displaystyle N}.
Title: SIR model anim
Credit: own image
Author: Phrontis
Usage Terms: Creative Commons Attribution-Share Alike 3.0
License: CC BY-SA 3.0
License Link: https://creativecommons.org/licenses/by-sa/3.0
Attribution Required?: Yes